运筹学-LP线性规划建模Lindo练习
豆豆 2022-12-21 21:10:00 1222人已围观
第一、Lindo 求解练习:
1、PPT DMD1-p14例1
例1:某工厂在生产过程中需要使用浓度为80%的硫酸100 吨,而市面上只有浓度为30%,45%,73%,85%,92%的硫酸出售, 每吨的价格分别为400、700、1400、1900和2500元。 问:采用怎样的购买方案,才能使所需总费用最小?
解答:
(1)、建模
设30%~92%的采购量为Xi(i=1,2,3,4,5)
目标函数:
min(z)=400X1+700X2+1400X3+1900X4+2500X5
约束条件:
X1+X2+X3+X4+X5=100;
30%X1+45%X2+73%X3+85%X4+92%X5=80%*100;
Xi>=0,(i=1,2,3,4,5)
(2)、Lindo求解
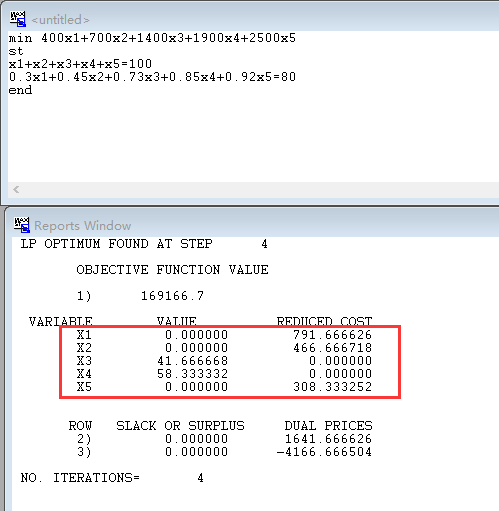
(3)、答案解析
X1=0,X2=0, X3=41.666668,X4=58.333332,X5=0;
MIN(Z)=169166.7
2、p20例5: 一家昼夜服务的饭店,24小时中需要的服务员数如下表所示。每个服务员每天连续工作8小时,且在时段开始时上班。问:最少需要多少名服务员?试建立该问题的线性规划模型。
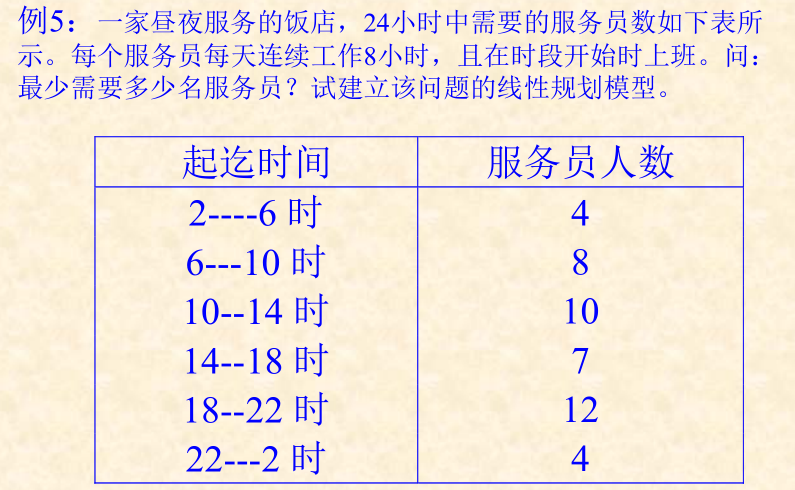
解答:
(1)、建模
变量设置如下:
| 上班时段 | 人员人数变量 | 下班时段 | 时段人数总量 | 需求人数 |
| 2--6 | X1 | 10-14 | X1+X6 | 4 |
| 6--10 | X2 | 14--18 | X1+X2 | 8 |
| 10--14 | X3 | 18--22 | X2+X3 | 10 |
| 14-18 | X4 | 22--2 | X3+X4 | 7 |
| 18-22 | X5 | 2--6 | X4+X5 | 12 |
| 22--2 | X6 | 6--10 | X5+X6 | 4 |
目标函数:
min(z)=X1+X2+X3+X4+X5+X6
约束条件:
X1+X6>=4
X1+X2>=8
X2+X3>=10
X3+X4>=7
X4+X5>=12
X5+X6>=4
Xi>=0,(i=1,2,3,4,5,6)
(2)、求解
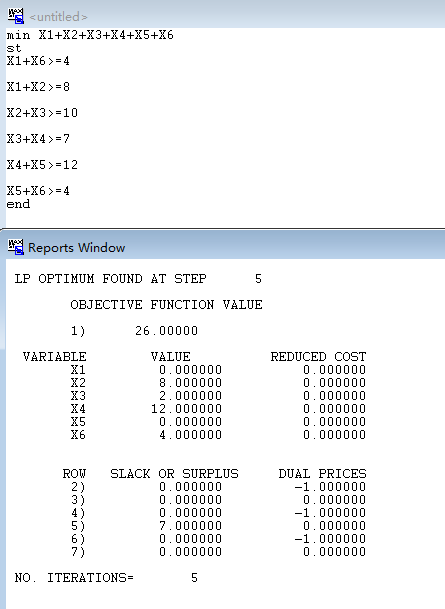
(3)、答案
X1=0;X2=8;X3=2;X4=12;X5=0;X6=4;
MIN(Z)=26
第二、EXCEL 求解练习:
PPT DMD1-p15例2

为了方便理解我把题目重新解释了一遍:
假设投资者有如下四个投资的机会.
(A)在三年内,投资人应在每年的年初投资,每年每元投资可获利息0.2元,每年取息后可重新将本息投入生息.
(B)在三年内,投资人应在第一年年初投资,每两年每元投资可获利息0.5元.两年后取息,可重新将本息投入生息.这种投资最多不得超过2万元.()
(C)在三年内,投资人应在第二年年初投资,两年后每元可获利息0.6元,这种投资最多不得超过1.5万元.
(D)在三年内,投资人应在第三年年初投资,一年内每元可获利息0.4元,这种投资不得超过1万元.假定在这三年为一期的投资中,每期的开始有3万元的资金可供投资,
投资人应怎样决定投资计划,才能在第三年底获得最高的收益.
理解分歧点
1、上一年投资到期的钱需要给到下一期作为启动资金,例如X11连本带利需要给X21和X23进行投资,X21+X12连本带利作为第三年启动资金给X31+X34注入资金
2、第三年底获得最高的收益有2种表达方式:第一是连本带利最大化,第二、利息最大化,本质没啥区别。
便于理解我做了一张题目的对应年限投资资金表格
| 第一年 | 第二年 | 第三年 | 第四年 | |
| A项目-0.2利率 | X11 | X21 | X31 | 取出 |
| B项目-0.5利率 | X12 | 取出用于其他方案投资 | ||
| C项目-0.6利率 | 不投资 | X23 | 取出 | |
| D项目-0.4利率 | 不投资 | 不投资 | X34 | 取出 |
解答
基于对题目的理解我认为可以用2个方式建模求解,第一种是利息最大化,第二种是本金+利息最大化
(1)、利息最大建模
设Xij为第i(i=1,2,3)年年初j(j=1,2,3,4)次投资金额
甲(A)方案第三年底获利:0.2(X11+X21+X31)
乙(B)方案第三年底获利:0.5X12
丙(C)方案第三年底获利:0.6X23
丁(D)方案第三年底获利:0.4X34
利息最大目标函数:
max(z)=0.2(X11+X21+X31)+0.5X12+0.6X23+0.4X34
约束条件:
X11+X12<=30000 (启动资金只有3万)
X21+X23<=1.2X11 (第二年的启动资金只有X11一个资金来源)
X21+X23<=30000-X12+0.2X11
X31+X34<=1.2X21+1.5X12
X31+X34<=30000-X23+0.2(X11+X21)+0.5X12
X12<=20000
X23<=15000
X34<=10000
Xij>=0(i=1,2,3;j=1,2,3,4)
规范后的约束条件:
X11+X12<=30000
X21+X23-1.2X11<=0
X21+X23<=30000-X12+0.2X11
X31+X34-1.2X21-1.5X12<=0
X31+X34<=30000-X23+0.2(X11+X21)+0.5X12
X12<=20000
X23<=15000
X34<=10000
Xij>=0(i=1,2,3;j=1,2,3,4)
(2)、lindo求解
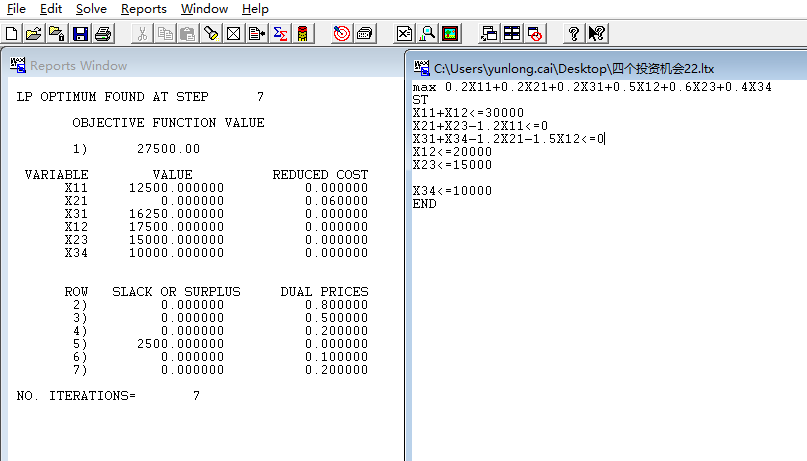
(3)、excel求解
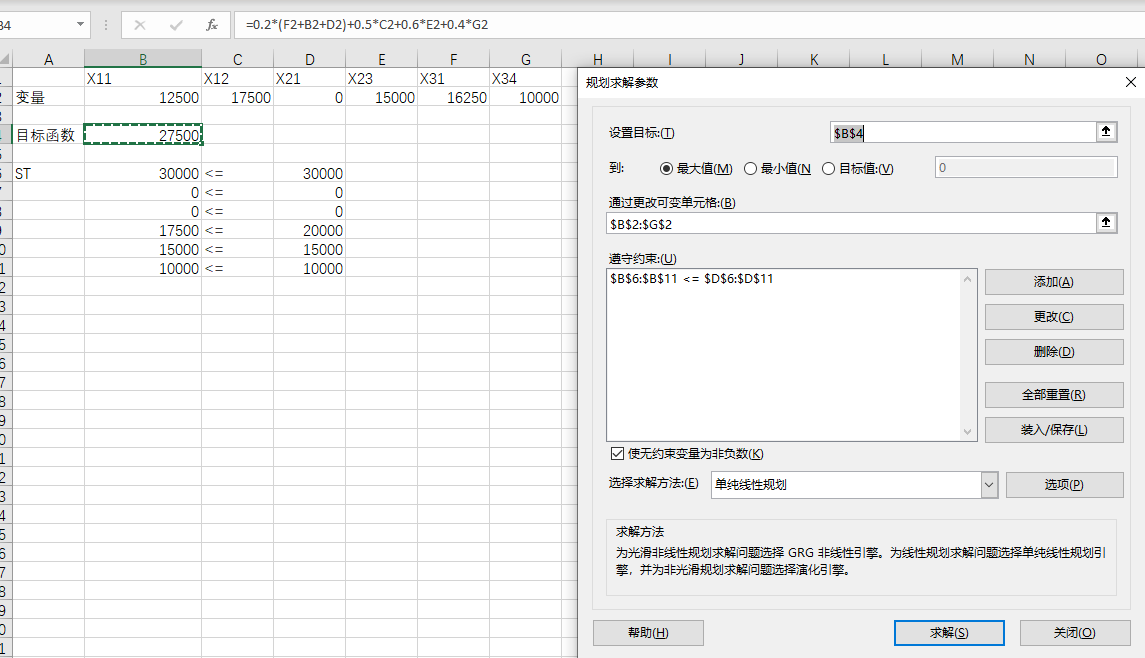
(4)、最优解
max(z)= 27500.00
X11 =12500.00
X21 =0.00
X31 =16250.00
X12 =17500.00
X23 =15000.00
X34 =10000.00
p17例3:要制作100套钢筋架子,每套含2.9米、2.1米、1.5米的钢筋各一根。已知原料长7.4米,问:如何下料,使用料最省?
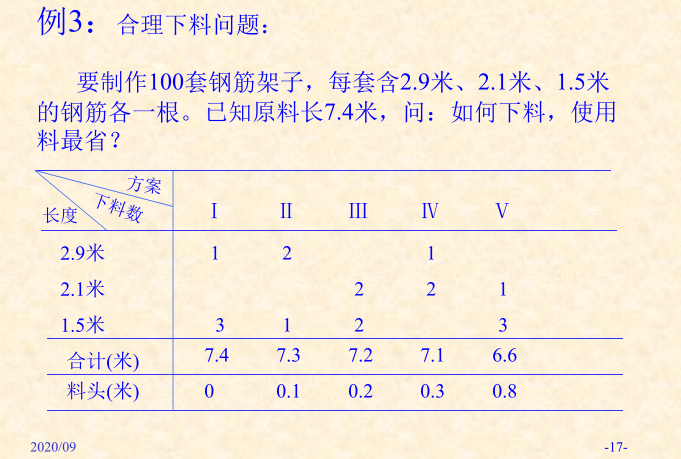
解答:
(1)、建模
设方案1-5的使用量分别为Xi(i=1,2,3,4,5),则
建模方案1:浪费最少
目标函数:
min(z)=0X1+0.1X2+0.2X3+0.3X4+0.8X5
约束条件:
X1+2X2+X4>=100
2X3+2X4+X5>=100
3X1+X2+2X3+3X5>=100
Xi>=0(i=1,2,3,4,5)
建模方案2:总钢材数量最小
目标函数:
min(z)=X1+X2+X3+X4+X5
约束条件:
X1+2X2+X4>=100
2X3+2X4+X5>=100
3X1+X2+2X3+3X5>=100
Xi>=0(i=1,2,3,4,5)
(2)、求解
方案1:浪费最小化
lindo求解

excel求解:
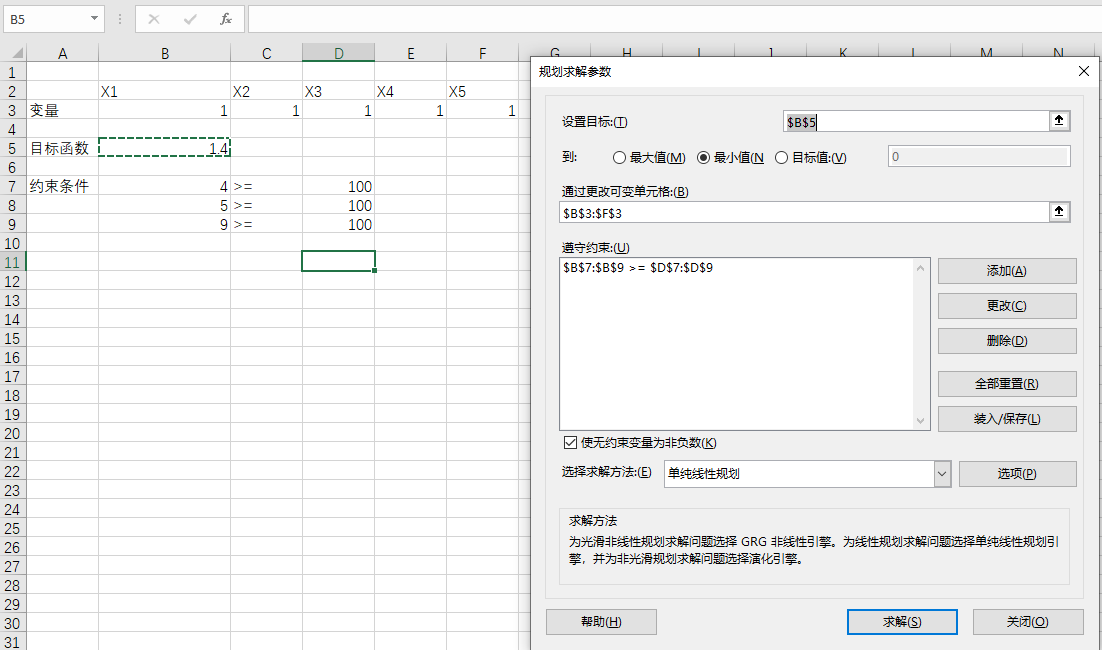
最优解:
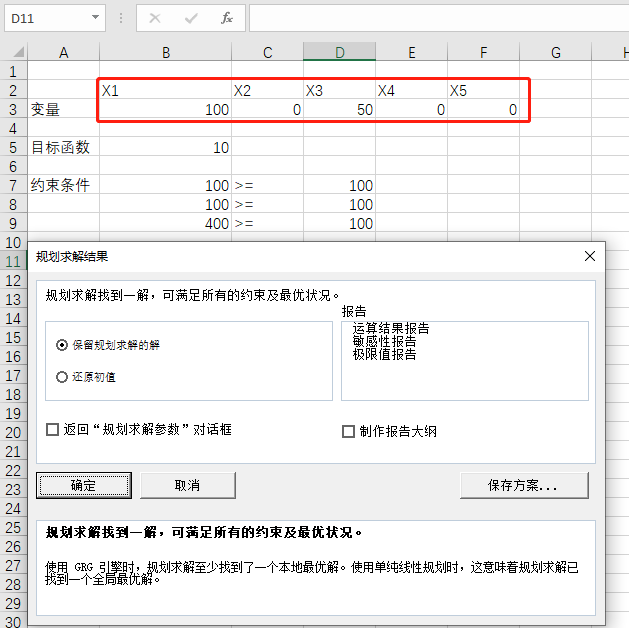
方案2:合理利用最大化
lindo求解
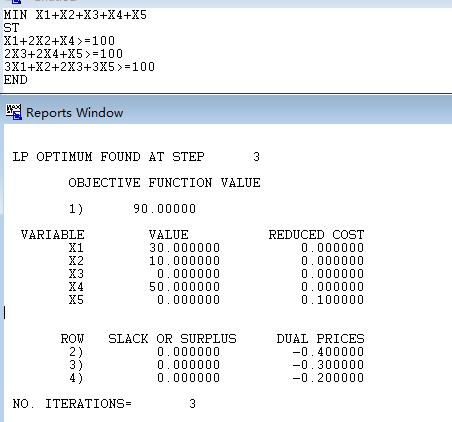
excel求解
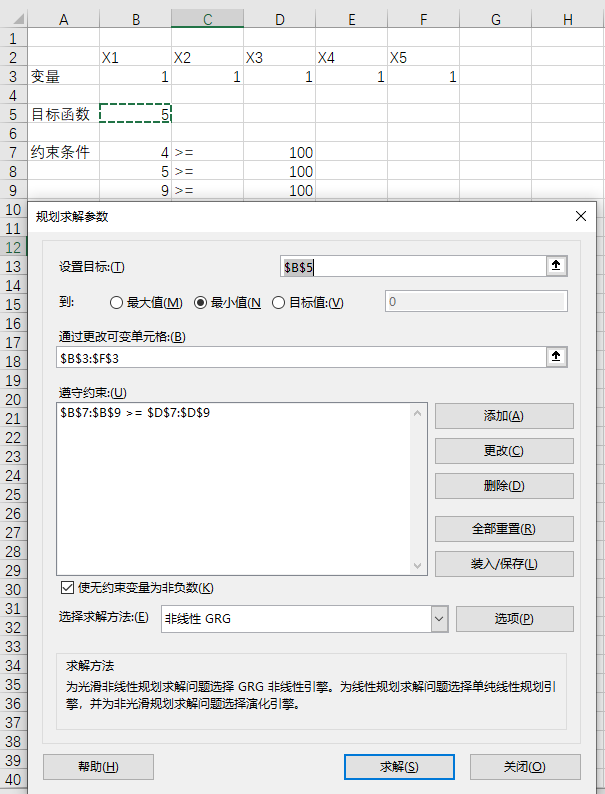
(3)、最优解
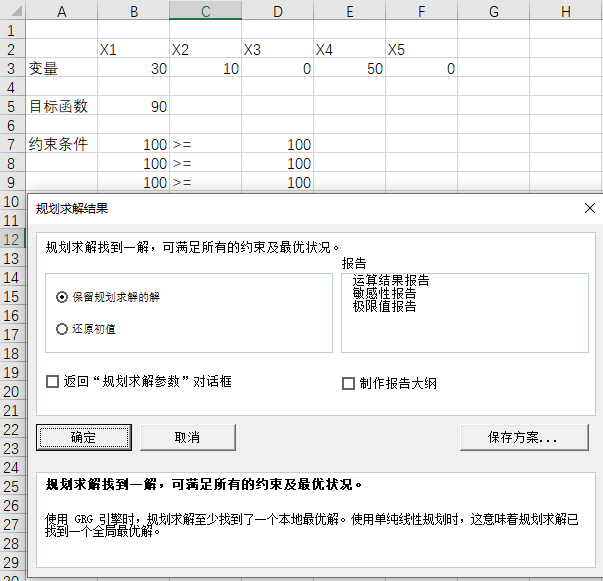
第三、参考答案
1、https://www.onekbit.com/dwz/232

 备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客
备付金存管银行是指可以为支付机构办理客户备付金的跨行收付业务,并负责对支付机构存放在所有备付金银行的客户备付金信息进行归集、核对与监督的备付金银行。(支付机构客 最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这
最近有一套生产系统的数据库CPU老是偏高,发现闲时也在40%-60%左右,感觉很不正常,决定优化一下,在这 首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽
首先需要知道什么叫一元购? 就是你支付一元后获得一个购物资格,有的叫抽